[CA3] Arithmetic for Computers

3.1. Introduction

Fractions and real numbers?

Overflow?

How does HW really multiply or divide numbers?

3.2. Addition and Subtraction

Terms

• Arithmetic Logic Unit (ALU)

  HW that performs addition, subtraction, and usually logical operations (such as AND and OR).

• exception (= interrupt)

  An unscheduled event that disrupts program execution (e.g. to detect overflow)

• interrupt

  An exception that comes from outside of the processor.

Algorithms

• Subtraction:
  • Add negation of second operand.
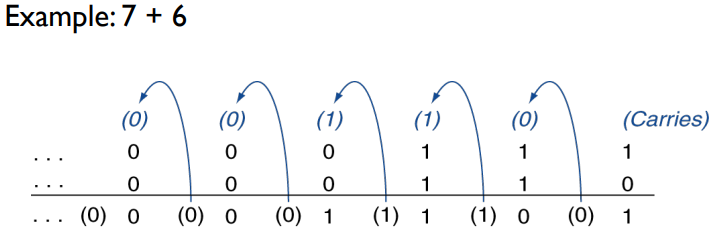
  • e.g. 7 - 6 = 7 + (-6)
• Addition:
  • Starting from the rightmost bit to the left, do the following:
    • input: carry ‘input’, op1, op2 (all bits) (carry ‘input’ of the rightmost bit is 0.)
    • output:
      • carry out: 1 iff 2 or more of them are 1.
      • the sum bit: 1 iff only 1 or 3 of them are 1.

Simple Adder (n-bit ripple-carry adder)

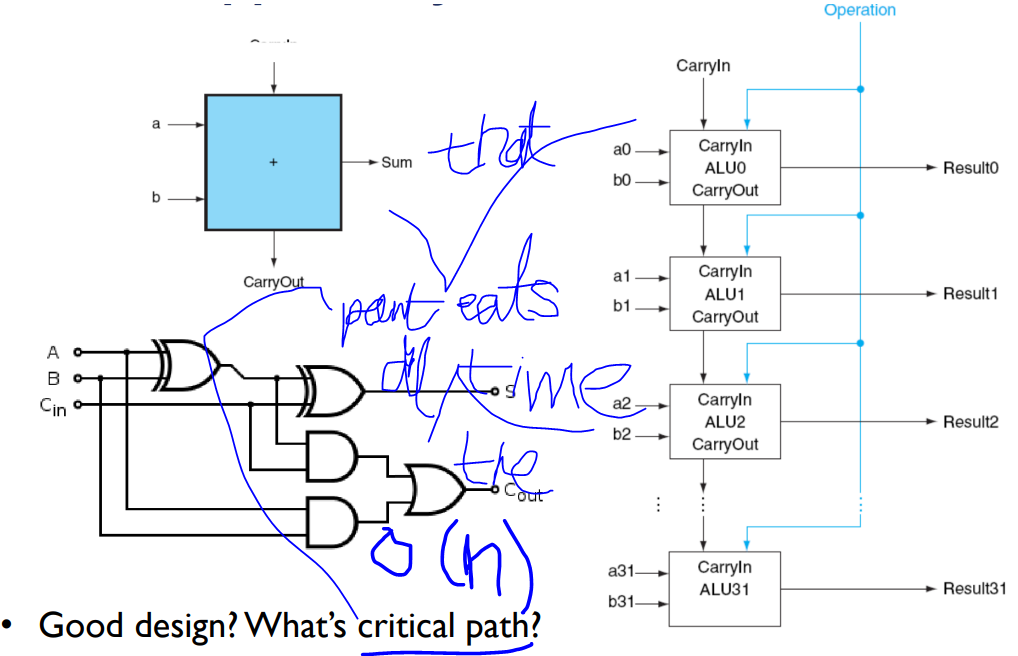
Critical Path? IDK!!! (part of some implementation that eats all the time)

Overflow: When result from an operation cannot be represented with the available HW. (a 32-bit word.)

Overflow Condition:

• (+) + (-) -> No overflow.
• (+) + (+) -> MSB == 1
• (-) + (-) -> MSB == 0

e.g. 7 - 6 is NOT an overflow (even if the 33rd carry exists).

MIPS instruction event on overflow:

• add, addi, sub: cause exceptions.

  e.g. Ada, Fortran: Require raising an exception

• addu, addiu, subu: cause no exceptions

  e.g. C

Nyum.

u: NO exception ilban: exception (overflow)

cf. Exception step?

• Save PC in exception program counter (EPC) register
• Jump to predefined handler address.
• mfc0 (move from coprocessor reg) instruction can retrieve EPC value, to return after corrctive action.

3.3. Multiplication

Multiply in MIPS

MIPS has two 32-bit registers to contain the 64-bit product:

• HI: most significant 32 bits
• LO: least significant 32 bits

Instructions:

• mult rs, rt / multu rs, rt

  64-bit prod in HI/LO

• mfhi rd / mflo rd

  move from HI/LO to rd. Can test HI => see if the product overflows 32 bits

• mul rd, rs, rt

  a pseudoinstruction that stores to rd the least significant 32 bits of product.

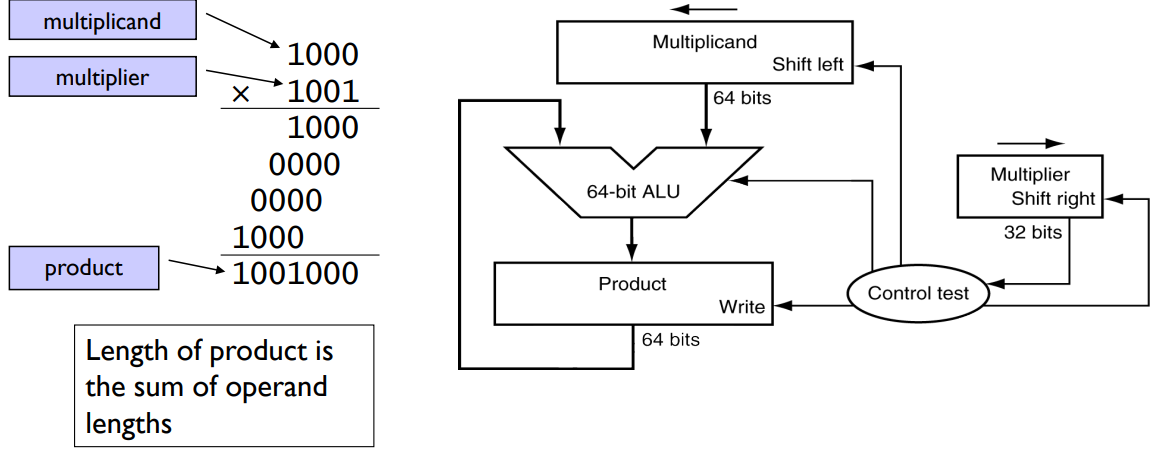
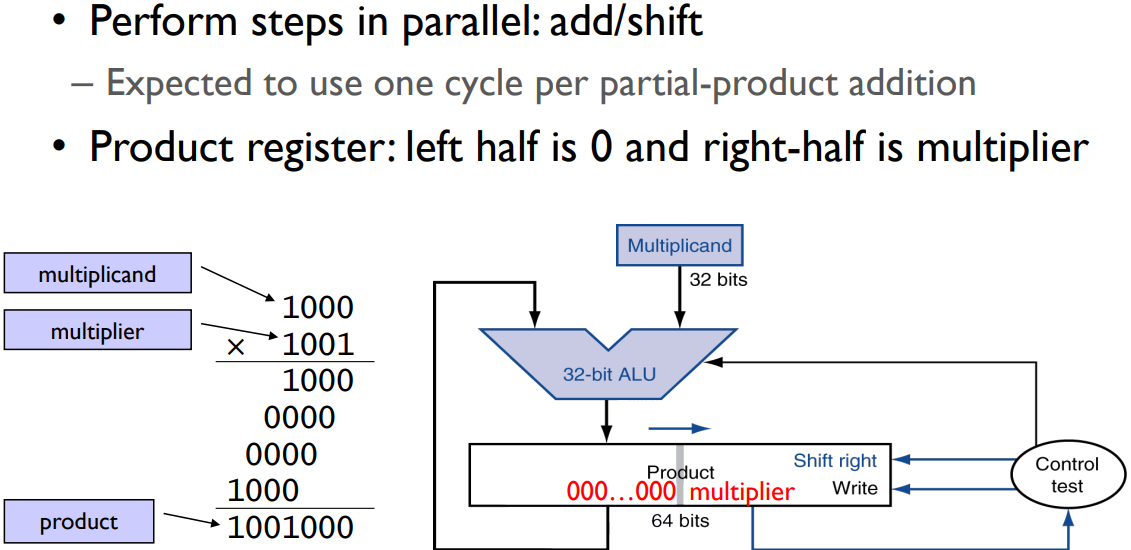
Simple Multiplier

2 operands:

• multiplicand (1st one)
• multiplier (2nd one)

1 output:

• product

• rectangle indicates the register.

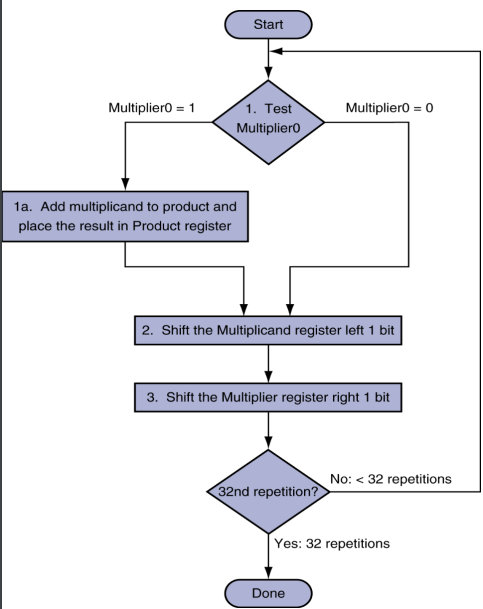
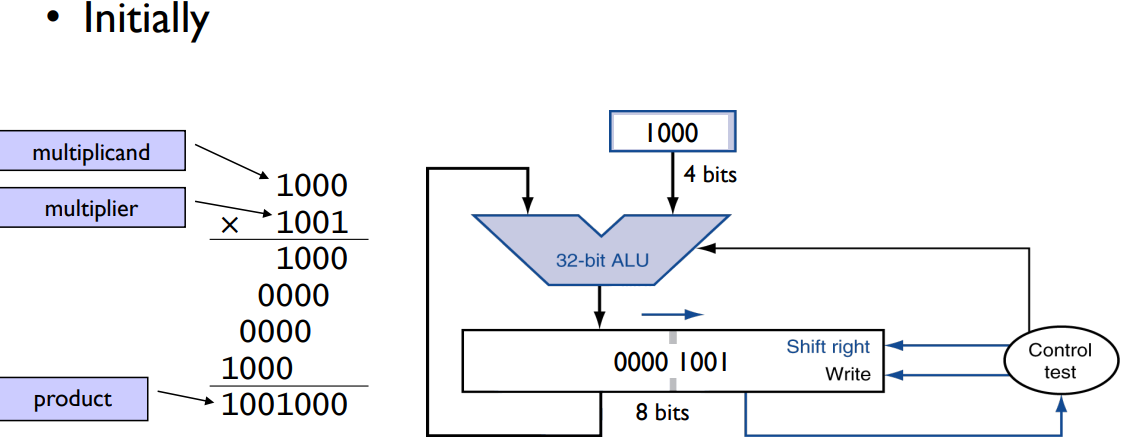
Algorithm

• product is initially zero.

Example

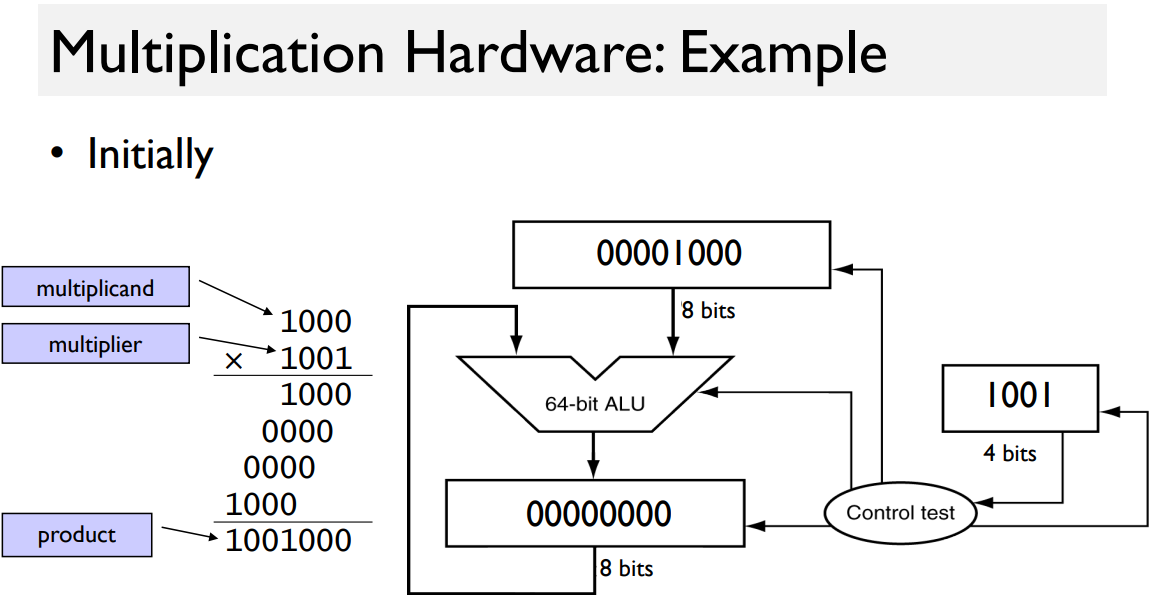
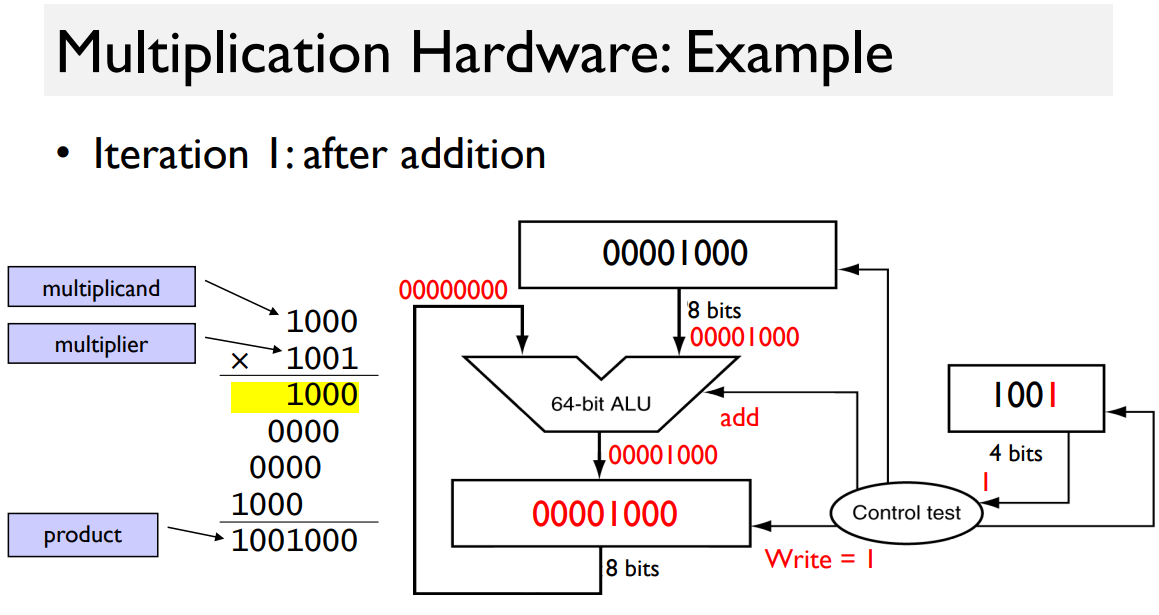
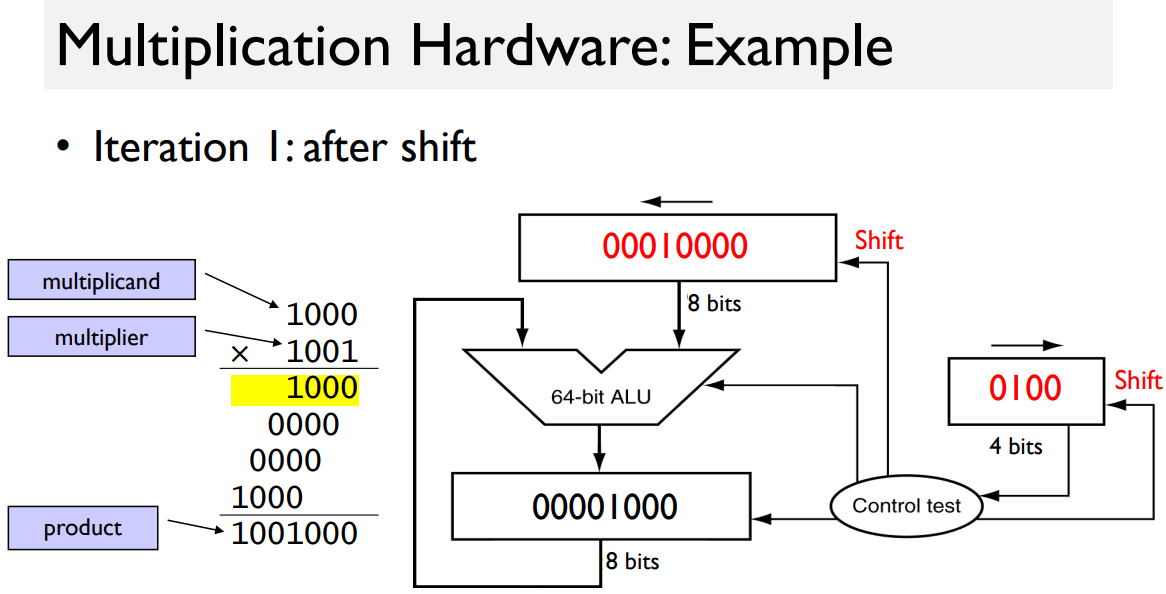
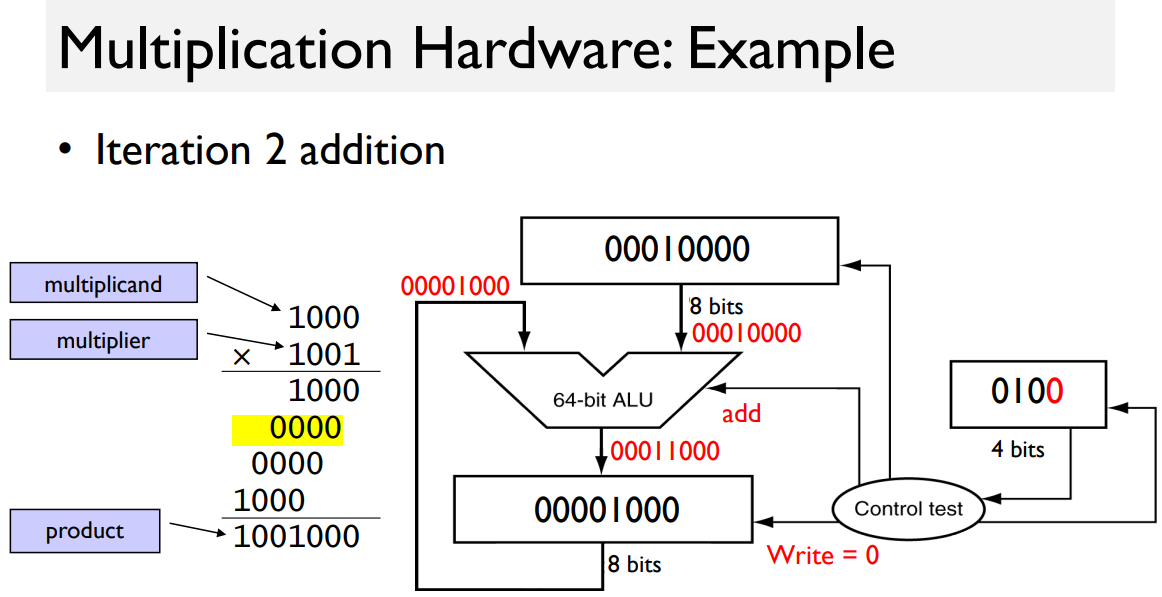
(“ALU: 8-bit, not 64”)

rest: see the print.

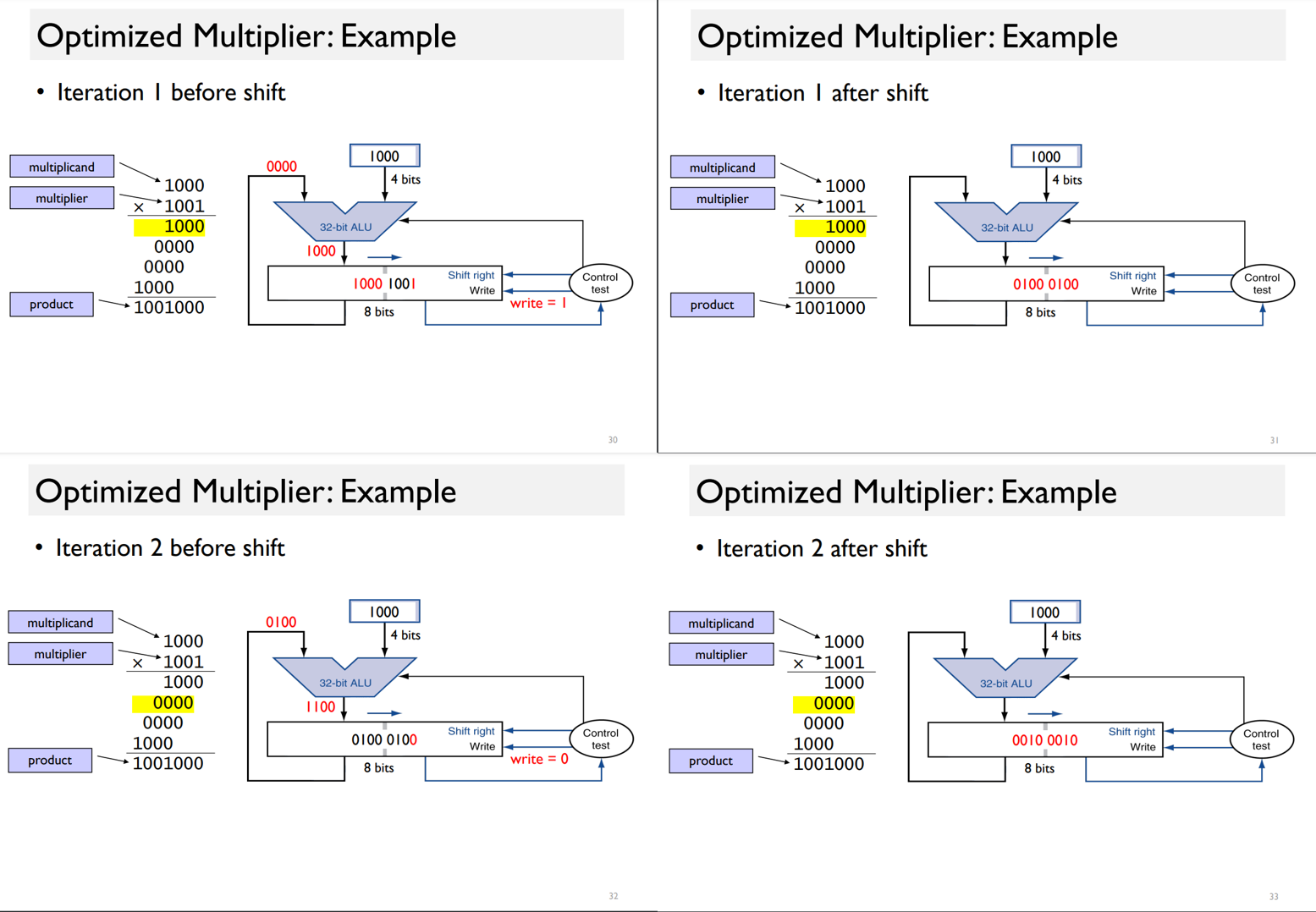
Optimized Multiplier

First one: Pipeline add and shift step

pipeline add and shift step. => in one clock cycle.

Faster Multiplier (up to: (log N) (N: # of bits))

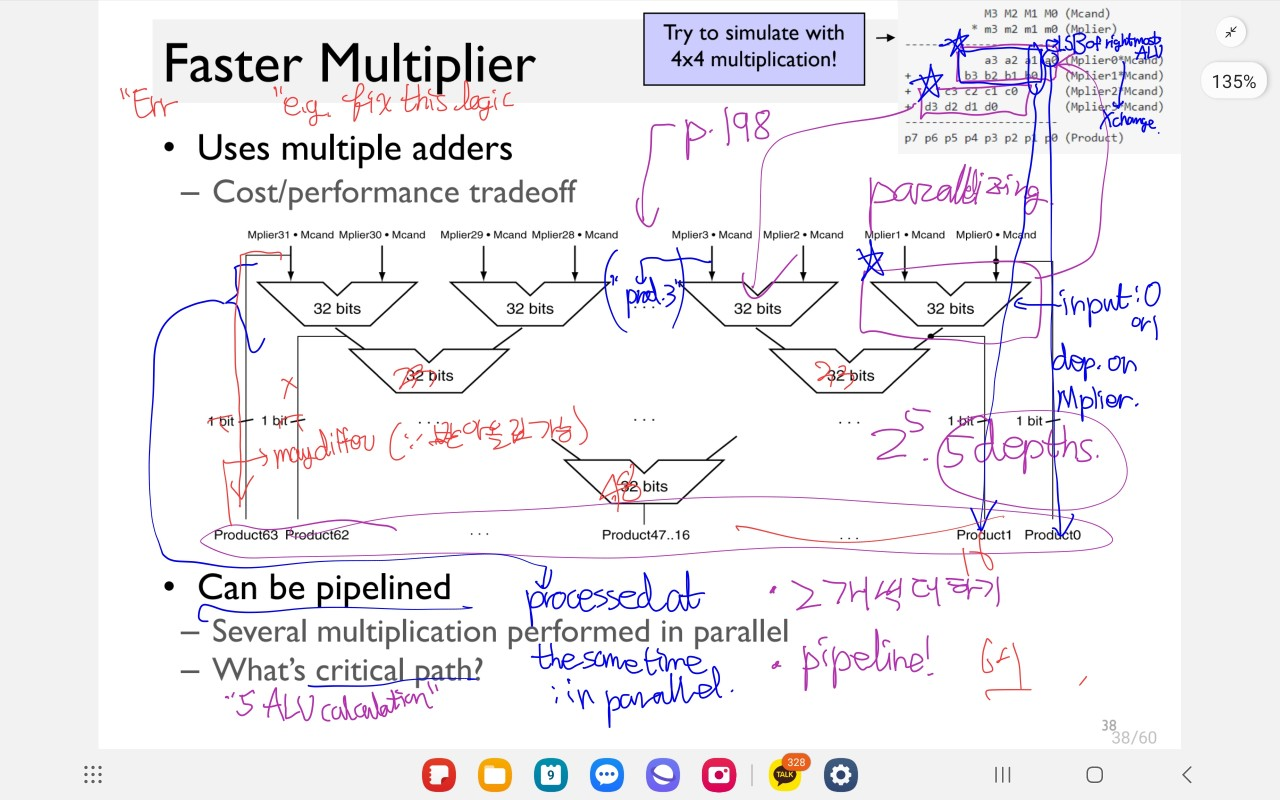
문제점

• 덧셈에서 받아올림을 통해 나오는 숫자가 더 커질 수 있다. 그러면 overflow가 발생한다.

e.g. 1101 * 11

_110	1 (4비트)
1101	_ (4비트)
=>10011	1 (5(>4)비트	1비트)

4비트 word로 표현 => 0011 (10011은 표현 불가!)

solution: 저걸 wordsize in bits + depth bit로 고친다.

e.g. 첫 ALU 결과는 33 bit, 둘째는 34, …, 마지막 5째 결과는 37 bit) 로 고치면 대충은 될 것 같다…

• MSB는 한 번의 덧셈 이후로도 달라질 수 있다.

  : e.g. 1101 * 1010

  => 11010 11010

  => 달라질 수 있다. (하지만 overflow때문에 그러지 못한다…)

3.4. Division

terms:

• dividend: A number being divided
• divisor: A number that the dividend is divided by.
• quotient: Th primary result of a division; a number that when multiplied by the divisor and added to the remainder produces the dividend.
• remainder: The secondary rsult of a division; a number that when added to the product of the qotient and the divisor producs the dividend.

Approaches

• Check for 0 divisor.
• Long division approach
  • divisor <= dividend bits
    • 1 bit in quotint, subtract, bring down next dividend bit
  • Else
    • 0 bit in quotient, bring down next dividend bit.

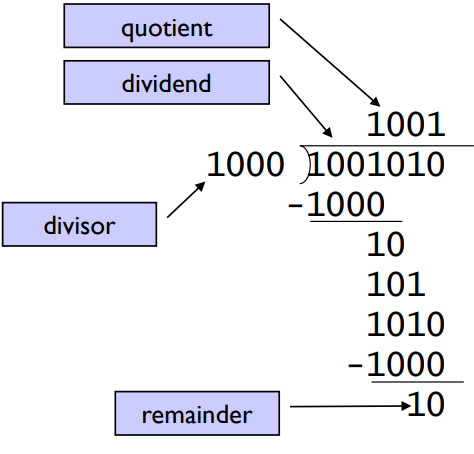
• Restoring division
  • Do the subtract first, and if remainder goes < 0, then add divisor back.

• Signed division
  • Divide using absolute values, adjust sign of quotient and remainder as required.

Algorithms

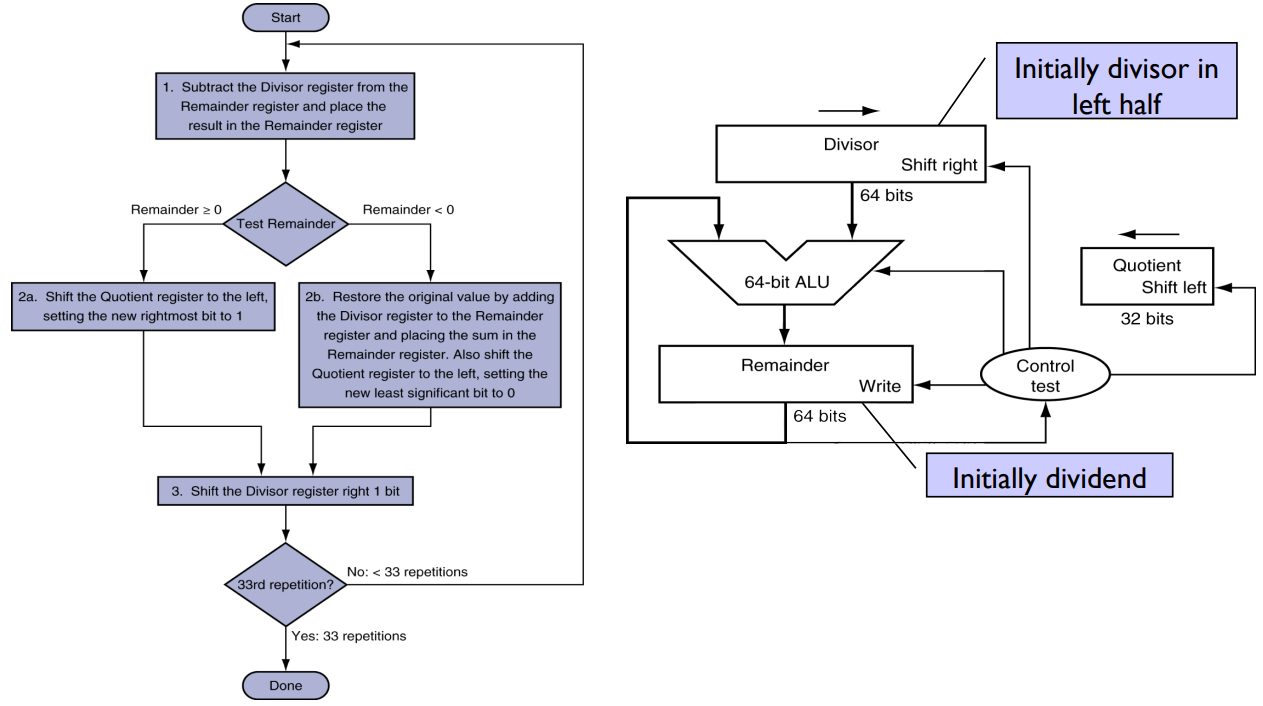
Restoring Division

See the print. Now you know it!

()

Optimized Divider

Just see it. That’s it.

MIPS instructions

• div $s2, $s3 : Lo = $s2 / $s3, Hi = $s2 mod $s3. (Lo = quotient, Hi = remainder)
• divu $s2, $s3 : nyumnyum. Unsigned quotient and remainder

3.5. Floating Point

terms

• scientific notation: A notation that renders numbers with a single digit to the left of the decimal point.
• normalized: A number in floating-point notation that has no leading 0s.
• floating point: Computer arithmetic that represents numbers in which the binary point is not fixed.
• fraction (a.k.a. the mantissa): The value, generally between 0 and 1, placed in th fraction field.
• exponent: The value that is placed in the exponent field in the numerical representation system of floating-point arithmetic.
• overflow (floating point) : A situation in which a positive exponent becomes too large to fit in the exponent field.
• underflow (floating point) : A situation in which a negative exponent bcomes too large to fit in the exponnt field.
• double precision : A floating-point value represented in two 32-bit words.
• single precision : A floating-point value represented in a single 32-bit word.
• guard: The first of two extra bits kept on the right during intermediate calculations of floating-point numbers; used to improve rounding accuracy.
• round: Method to make the intermediate floating-point result fit the floating-point format; the goal is typically to find the nearest number that can be represented in the format.
• units in the last place (ulp) : The number of bits in error in th LSBs of the significand between the actual number and the number that can be represented.
• sticky bit: A bit used in rounding in addition to guard and round that is set whenever there are nonzero bits to the right of the round bit.
• fuzed multiply add: A floting-point instruction that performs both a multiply and an add, but rounds only once after the add.

Floating Point Representation

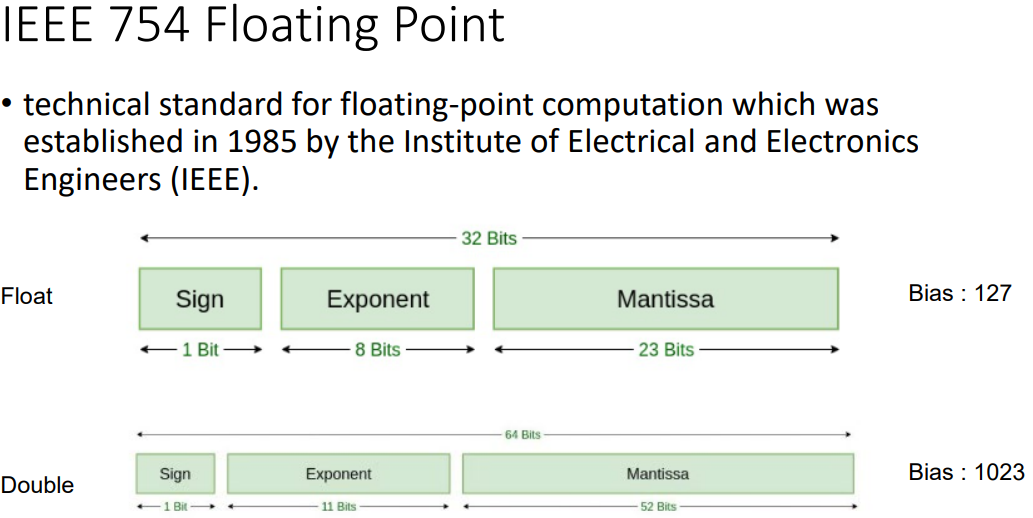
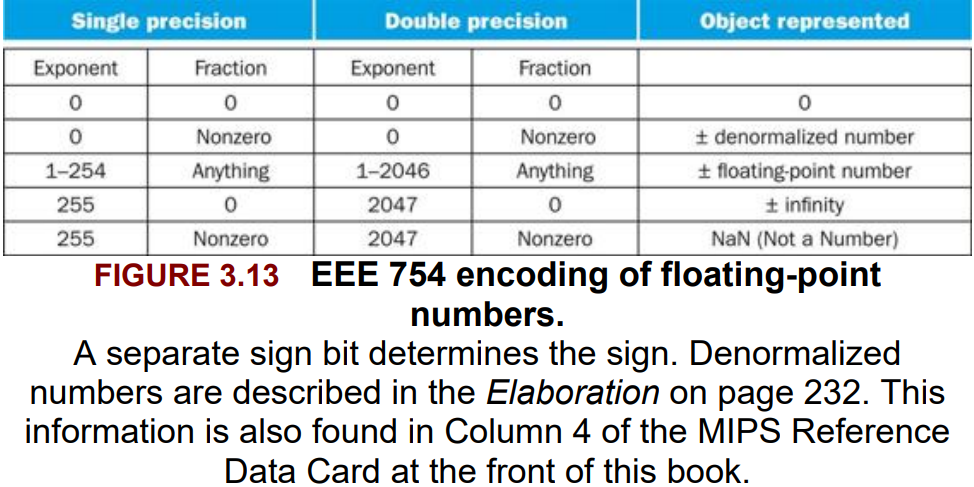
Fields of Floating Point numbers

• sign bit (1)
• exponent (8) or (11)
• fraction (23) or (20+32)

Here’s a basic overview of how floating-point numbers work:

1. Sign bit

   The leftmost bit (bit 0) is the sign bit. It determines whether the number is positive or negative. 0 represents a positive number, and 1 represents a negative number.

2. Exponent

   The next set of bits represents the exponent. This part determines the magnitude of the number and where the decimal point is located. The exponent is biased, meaning a fixed value is added to it to ensure positive values are greater than or equal to zero. The bias value is typically set to 127 or 1023, depending on the floating-point format (single precision or double precision).

3. Fraction (or Mantissa)

   The remaining bits represent the fractional part of the number. These bits store the precision or the significant digits of the number. The fraction is normalized, which means the leading bit is always 1, so it doesn’t need to be explicitly stored.

(-1)^S * 2^E * 1.F

• S is the sign bit.
• E is the exponent, after bias subtraction.
• F is the fractional part (mantissa), which represents the significant digits.

Here are a few key points to keep in mind:

• Floating-point numbers are inherently approximations of real numbers. Not all real numbers can be exactly represented using this system.
• Floating-point arithmetic can introduce rounding errors, which can accumulate in complex calculations, potentially leading to inaccuracies.
• Floating-point numbers have limited precision. Single-precision (32-bit) and double-precision (64-bit) formats are common, but there are also extended precision and quadruple-precision formats for higher precision when needed.
• Special values include positive and negative infinity, NaN (Not-a-Number), and denormalized numbers, which are used to represent exceptional cases.
• Conversion between decimal and binary floating-point representations can sometimes lead to loss of precision, especially when converting from decimal to binary.

Programmers should be aware of these characteristics when using floating-point numbers in their applications and consider using appropriate rounding techniques and error-handling strategies to mitigate potential issues.

Example: Floating-Point Representation

Represent -0.75 in single and double precision.

Sol

It’s also -3/4.

In Binary Fraction, -11/2^2

Scientific notation => -0.11 * 2^0.

Normalized Scientific Notation => -1.1 * 2^-1

• single precision representation

  • s(1) = 1

  • exp(8) = (-1)+127 = 126

  • fraction(23) = .100000…0

  \[(-1)^1 * (1 + .1000 0000 0000 0000 0000 000) * 2^{(126-127)}\]

  Ans: [1 01111110 1(0*22)]

• double precision:

  • s(1) = 1

  • exp(11) = (-1)+1023 = 1022

  • fraction(52) = .100000…0

  Ans: [1 01111111110 1(0*19) (0*32)]

Example: Converting Binary to Decimal Floating Point

What decimal number is this single precision float representing?

1 10000001 0100 0000 0000 0000 000

Sol

\[(-1)^1 * (1+.0100 0000 0000 0000 000) * 2^{129-127} = -1.25 * 2^2 = -5.0\]

Ans

-5.0

Floating-Point Addition

Algorithm

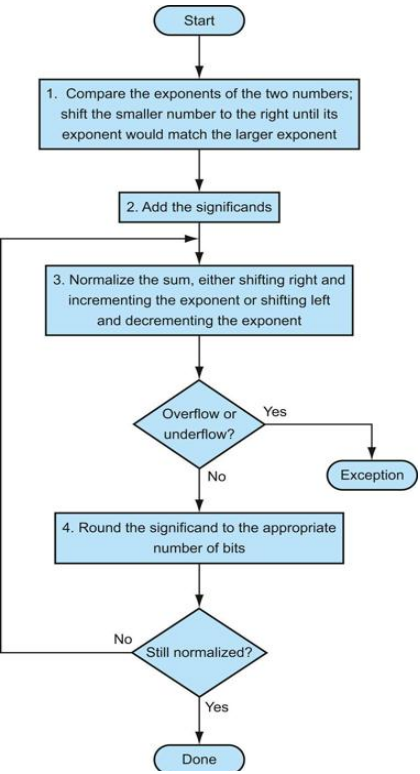
Example: Binary Floating-Point Addition

Try adding the numbers 0.5 (ten) and -0.4375 (ten) in binary using the algorithm in figure 3.14.

Sol

1. Convert the two numbers into floating-point numbers.

• 0.5(ten) = 1.0(bin) * 2^-1. => (Sign, Exp, Fraction) = (0, 126, 0000 0000 0000 0000 0000 000)

• -0.4375(ten) = -1 * 1.11 * 2^-2. => (Sign, Exp, Fraction) = (1, 125, 1100 0000 0000 0000 0000 000)

1. Convert two floating-point numbers into binary scientific representation

• (0, 126, 0), (1, 124, 11) -> (0, 126, 0), (1, 126, 0011) (X)

• (0, 126, 0) => 1.0 * 2^-1, (1, 125, 11) => -1.11 * 2^(-2)

1. Apply the algorithm.

(1.0 - 0.111) * 2^-1 = 0.001 * 2^-1. (match the common exponent to larger one & add the “significands”)

= 1.0 * 2^-4 (Normalize the sum)

Check Overflow/Underflow (-127 <= -4 <= 128). : No over/underflow.

(Round the Sum) : Same.

Thus, the sum is 0.0625(ten).

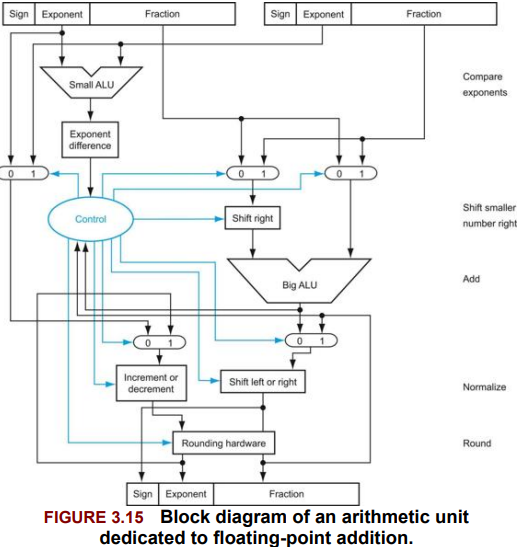
The steps of Figure 3.14 correspond to each block, from top to bottom. First, the exponent of one operand is subtracted from the other using the small ALU to determine which is larger and by how much. This difference controls the three multiplexors; from left to right, they select the larger exponent, the significand of the smaller number, and the significand of the larger number. The smaller significand is shifted right, and then the significands are added together using the big ALU. The normalization step then shifts the sum left or right and increments or decrements the exponent. Rounding then creates the final result, which may require normalizing again to produce the actual final result.

Floating-Point Multiplication

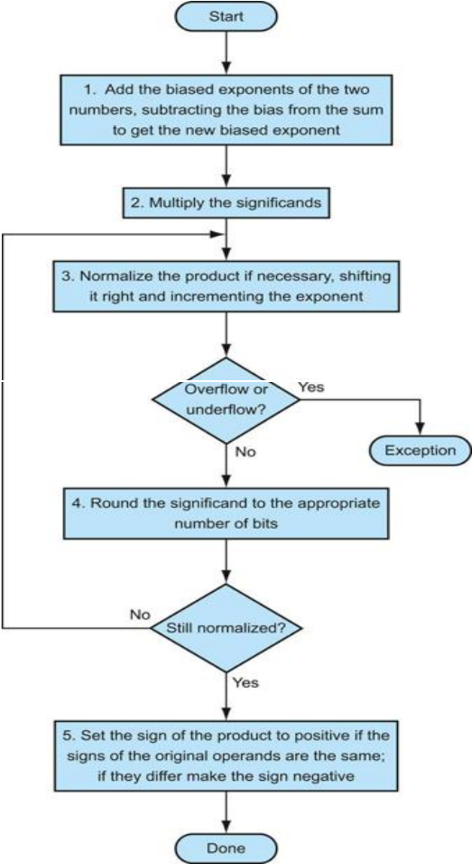
Algorithm

The normal path is to execute steps 3 and 4 once, but if rounding causes the sum to be unnormalized, we must repeat step 3.

Example: Binary Floating-Point Multiplication

multiply the numbers 0.5_ten and -0.4375_ten, using the steps in the figure.

Sol:

In binary, the task is multiplying \(1.0_{two} * 2^{-1}\) by \(- 1.110_{two} * 2^{-2}\)

MIPS Floating-Point Instructions

Registers

• $f0, $f1, … used either for single / double precision. (double: use in pair.)

Instructions (Floating-Point)

• add.s, add.d : addition, single and double
• sub.s, sub.d : subtraction, single and double
• mul.s, mul.d : multiplication, single and double
• div.s, div.d : division, single and double

• c.x.s, c.x.d : comparison, single and double

  Note that the x can be either…

  • eq
  • neq
  • lt
  • le
  • gt
  • ge

• bclt, bclf : branch on floating-point, true and false (??)

• lwc1 and swc1 : seperate loads and stores for floating-point registers.

Example: load two single precision numbers from memory, add, and store the sum

lwc1 $f4, c($sp)  #Load 32-bit F.P. number into F4
lwc1 $f6, a($sp)
add.s $f2, $f4, $f6
swc1 $f2, b($sp)

Accurate Arithmetic

3.6. Parallelism and Computer Arithmetic: Subword Parallelism

Word List

❗단어들❗

link	단어	뜻
1	instruction set	The vocabulary of commands understood by a given architecture
2	stored-program concept	The idea that instructions and data of many types can be stored in memory as numbers, leading to the stored program computer.
3	word	The natural unit of access in a computer, usually a group of 32 bits; corresponds to the size of a register in the MIPS architecture.
—	data race	Two memory accesses from a data race if they are from different threads to same location, at least one is a write, and thy occur one after another.
—	pseudoinstruction	A common variation of assembly language instructions often treated as if it were an instruction in its own right.